Математические основы индикаторов

[Lexxodessa]

стоящий автомобиль, тоже едет - во-времени
посмотрите на брошенные вдоль дорог автомобили... вокруг них, меняется все - люди, дома, города - и они движутся во времени, вместе со всеми
и водитель не давит на газ .....

это и называется - стабильность =)

Покажи движение .

 

[AlexeNP]

ну, раз про педали зашел разговор, то это дело рассматривал еще Винер. Давно это было, кому неохота всю книжку читать - страницы 29-31.
Время учитывается всегда, но чаще - неявно. Пример: положим, что цена двигается линейным трендом, тогда ее значение в момент t1 будет p1 = k*t1 + s
но, тогда в предыдущий момент t2 (нумерация как в тайм-сериях) цена будет p2 = k*t2 + s
делаем подстановку t1 = t2 + 1 (на единичку наш временной параметр увеличился), тогда
p1 = k*(t2+1) + s
p1 = k*t2 + s + k
теперь делаем еще одну подстановку, и получаем
p1 = p2 + k - время из уравнения пропало, но тем не менее оно есть) время не может не есть, хотя бы потому, что мы так или иначе работаем с последовательностями. Ярким примером такого подхода является фильтр Савицкого - Голея


дальше, Lexxodessa упомянул про уровни Фибоначчи... но это уже переход из временной области в область значений. Теоретически можно написать кучку разных уровней, но вот много ли желающих найдется чтобы их приобресть?

 

[AlexeNP]

на днях мне опять про уровни Фибоначчи напомнили... то ли закон парных случаев, то ли фрактальная динамика)
Ну, про Фибоначчи нам всё ясно - там кролики размножаются туда-сюда. А я человек старый, я как кролики уже не могу. Поэтому будем использовать упорядоченный логит.
Итак, собираем статистику по максимальным отклонениям от цены открытия на N баров вперед, а потом начинаем чертить уровни. Но для этого нужно выбрать единицу изменения. Для этого нам поможет размер спреда - он будет соответствовать плохим уровням и поэтому показывать не будем. А вот уровни ничё так, норм и хорошо - обязательно посмотрим



Итак, уровни зависят от того что творилось в истории и текущего спреда. Шаг увеличения можно подбирать как вам угодно (но больше ноля), количество уровней может быть каким угодно - максимальное отклонение ограничено наибольшим отклонением на истории, для особо щепетильных советую движения цены вверх и вниз учитывать раздельно.

 

[AlexeNP]

давно чего-то жесткого и кровавого у нас не было, поэтому сегодня речь пойдет про функцию выживания...

Эта песня о бедном рыбаке, который поплыл из Неаполя в бурное море. А его бедная девушка ждала на берегу, ждала-ждала, пока не дождалась. Она сбросила с себя последнюю одежду и тоже бросилась в бурное море. И сия пучина поглотила ея в один момент. В общем, все умерли.

Представьте, что есть некий трейдер который на открытии каждого бара запуливает два ордера - вверх, вниз, и вообще во все стороны, с некоторым - заранее установленным тейк-профитом. Его не волнует просадка и маржа - вот ведь гад какой.
Но нас не особо интересует его стиль торговли, но вот справочную информацию - типа сколько и каких ордеров у него сейчас открыто - нам интересно бы узнать. Объясняю почему - прикиньте, этот трейдер сообщает нам, что у него сейчас открыто скажем 50 ордеров Buy и 10 ордеров Sell. Вопрос: в какую сторону преимущественно двигался рынок?
Видите, как всё просто - много синих столбиков - цена шла вниз, много красных - вверх...

 

[MERFY]

на днях мне опять про уровни Фибоначчи напомнили... то ли закон парных случаев, то ли фрактальная динамика)
Ну, про Фибоначчи нам всё ясно - там кролики размножаются туда-сюда. А я человек старый, я как кролики уже не могу. Поэтому будем использовать упорядоченный логит.
Итак, собираем статистику по максимальным отклонениям от цены открытия на N баров вперед, а потом начинаем чертить уровни. Но для этого нужно выбрать единицу изменения. Для этого нам поможет размер спреда - он будет соответствовать плохим уровням и поэтому показывать не будем. А вот уровни ничё так, норм и хорошо - обязательно посмотрим

Посмотреть вложение 453065

Итак, уровни зависят от того что творилось в истории и текущего спреда. Шаг увеличения можно подбирать как вам угодно (но больше ноля), количество уровней может быть каким угодно - максимальное отклонение ограничено наибольшим отклонением на истории, для особо щепетильных советую движения цены вверх и вниз учитывать раздельно.

Алекс, нужно сделать их статичными, и будет отлично.

 

[AlexeNP]

за показатель Хёрста, очень кратенько... Конечно, показатель очень интересный с точки зрения посмотреть и подумать. Но вот считать его - ухи опухнут... С другой стороны, можно чего-нибудь приблизительное сварганить. Что тоже неплохо)


Dimension - размерность, в которой считается параметр. Насчет 3D я приврал, но тоже норм)
iPeriod - количество баров для расчета
При значениях больше 0.5 ряд считается персистентным - он сохраняет тренд, то есть возрастание в прошлом более вероятно приводит к возрастанию в дальнейшем, и наоборот. При значении 0,5 явной тенденции не выражено, а при меньших значениях процесс характеризуется антиперсистентностью — любая тенденция стремится смениться противоположной.

 

[Bullra]

на днях мне опять про уровни Фибоначчи напомнили... то ли закон парных случаев, то ли фрактальная динамика)
Ну, про Фибоначчи нам всё ясно - там кролики размножаются туда-сюда. А я человек старый, я как кролики уже не могу. Поэтому будем использовать упорядоченный логит.

Ну и зря. Ведь кролики - это не только вкусное мясо, но еще и ценный мех. Вот хомяки да. Это полный ПЭ! Впрочем... если завести питона, то ему могут понравится.

 

[IRIP]

Алекс, нужно сделать их статичными, и будет отлично.

а еще мультитаймфреймовыми

 

[AlexeNP]

а еще мультитаймфреймовыми

отвечу на оба вопроса сразу.
1) Статичность. Для расчета уровней нужно задать значение первого уровня. К примеру, мы хотим найти уровни "плохо", "средне", "хорошо" и т.д. и т.п. Для их расчета нужно значение "очень плохо". В данном случае естественным решением было принять за уровень "очень плохо" размер спреда. Поэтому, спред на месте - уровни тоже стоят как вкопанные, пляшет спред - уровни тоже на месте не стоят. Но если уж вам хочется неподвижности, то ладно...
2) Мультитаймфрейм - тут уже лучше надстройку делать к индикатору, чтобы статистика по истории учитывалась наверняка

 

[magistr91]

отвечу на оба вопроса сразу.
1) Статичность. Для расчета уровней нужно задать значение первого уровня. К примеру, мы хотим найти уровни "плохо", "средне", "хорошо" и т.д. и т.п. Для их расчета нужно значение "очень плохо". В данном случае естественным решением было принять за уровень "очень плохо" размер спреда. Поэтому, спред на месте - уровни тоже стоят как вкопанные, пляшет спред - уровни тоже на месте не стоят. Но если уж вам хочется неподвижности, то ладно...
2) Мультитаймфрейм - тут уже лучше надстройку делать к индикатору, чтобы статистика по истории учитывалась наверняка

Приветствую AlexeNP. А в истории никак не увидеть отрабатывались уровни или нет? Другими словами чтобы увидеть историю нужно чтобы если сегодня я установил на график индикатор то собрать историю нужно начиная с момента установки? Так?

 

[AlexeNP]

Приветствую AlexeNP. А в истории никак не увидеть отрабатывались уровни или нет? Другими словами чтобы увидеть историю нужно чтобы если сегодня я установил на график индикатор то собрать историю нужно начиная с момента установки? Так?

всё верно... нужна какая-то статистика.... чисто теоретически можно переделать в обычный индикатор, но ... пока индикатор не наберет достаточного количества данных, он будет показывать все что угодно) и (в МТ4) спред не сохраняется, поэтому исторические показы будут довольно приблизительными

 

[AlexeNP]

Как это не прискорбно, но с угловыми величинами бывает полный затык и неясность. А именно - даже расчет среднего угла может стать серьезной проблемой. Для примера, будем строить трендовую линию за N отсчетов. Для чего будем определять средний угол по всем парам точек, заодно посчитаем и среднее отклонение. В этом нам поможет свернутое нормальное распределение. А для работы с угловыми величинами нам потребуются синус, косинус, пытливый ум и шаловливые ручки.
В данном случае, я беру строго заданное значение начальной точки и начиная с нее нахожу средний угол по всем парам точек, которые находятся между началом и концом. В итоге получается примерно такая красота.

Для еще большей красивости можно использовать оценку Тейла-Сена, и конечно же сделать расчет начальной точки.

 

[Genry_05]

Как это не прискорбно, но с угловыми величинами бывает полный затык и неясность. А именно - даже расчет среднего угла может стать серьезной проблемой. Для примера, будем строить трендовую линию за N отсчетов. Для чего будем определять средний угол по всем парам точек, заодно посчитаем и среднее отклонение. В этом нам поможет свернутое нормальное распределение. А для работы с угловыми величинами нам потребуются синус, косинус, пытливый ум и шаловливые ручки.
В данном случае, я беру строго заданное значение начальной точки и начиная с нее нахожу средний угол по всем парам точек, которые находятся между началом и концом. В итоге получается примерно такая красота.
Посмотреть вложение 453416
Для еще большей красивости можно использовать оценку Тейла-Сена, и конечно же сделать расчет начальной точки.

Alex, Спасибо!
Читать Ваши математические новеллы - одно удовольствие
Жду продолжения , думаю что не один
Зы. В последнем индикаторе для iPeriod типа uchar маловато будет.
И string prefix="WND_"+(string)iPeriod
Тогда такая красотища будет

 

[AlexeNP]

Гляжу, кругом - благолепие и красота. Надоело, давайте сеять вокруг хаос и беспорядок. Раз есть гармоническое среднее, то должно быть и противогармоническое . И такое среднее есть и оно является частным случаем средних Лемера. Вот о них и будет данный индикатор.
Представьте, индикатор может работать и как обычное среднее, и как какой-то канальный... запросто. Что получится, зависит от параметра Exponent. 0 - смысла не имеет, 1 - обычная скользящая средняя, 2- контргармоничное среднее...
смотрим Exponent=2

ну, в общем - чего-то сглаживающее Да и нормально. Но картина начинает меняться при повышении Exponent. Вообще, это среднее может служит детектором огибающей по точкам экстремумов. Вот тут Лемер просил кланяться и передавать привет строителям зигзагов. Представьте, какие у вас будут зигзаги, если сначала вы отфильтруете максимумы и минимумы с помощью этой средней.
Итак, Exponent = 1000

 

[Genry_05]

[хрум]В данном случае, я беру строго заданное значение начальной точки и начиная с нее нахожу средний угол по всем парам точек, которые находятся между началом и концом. В итоге получается примерно такая красота.
Посмотреть вложение 453416
Для еще большей красивости можно использовать оценку Тейла-Сена, и конечно же сделать расчет начальной точки.

Если от заданного локального экстремума начинается тренд, то можно полученный вектор попробовать применить к остальным экстремумам тренда.
Получилось так. Напоминает Вилы Эндрюса..., но построение отличается

 

[vladavd]

p1 = p2 + k - время из уравнения пропало, но тем не менее оно есть) время не может не есть, хотя бы потому, что мы так или иначе работаем с последовательностями. Ярким примером такого подхода является фильтр Савицкого - Голея

Работать с временной последовательностью, а не с графиком качественной характеристики процесса (ампер-часы, литры бензина, самосвалы с песком, торговый объем) можно, но чревато низкой точностью, а часто и катастрофически низкой. Мы же при таком подходе не измеряем конкретное состояние, а оперируем неким средним типичным состоянием, которое, полагаясь на авось и на так сойдет, решаем считать универсальным. Разница получается примерно как между средней температурой по больнице и температурой одного конкретного больного. Ну или как варить суп не до готовности, а ровно час, как в рецепте написано; причем не глядя на конфорку, а там то полный газ, то он вообще даже не включен.

 

[AlexeNP]

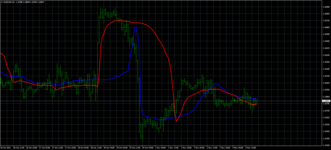
Работать с временной последовательностью, а не с графиком качественной характеристики процесса (ампер-часы, литры бензина, самосвалы с песком, торговый объем) можно, но чревато низкой точностью, а часто и катастрофически низкой. Мы же при таком подходе не измеряем конкретное состояние, а оперируем неким средним типичным состоянием, которое, полагаясь на авось и на так сойдет, решаем считать универсальным. Разница получается примерно как между средней температурой по больнице и температурой одного конкретного больного. Ну или как варить суп не до готовности, а ровно час, как в рецепте написано; причем не глядя на конфорку, а там то полный газ, то он вообще даже не включен.

че ж все так сложно-то у вас?
ладно поехали сначала...
у нас есть некий процесс, который развивается во времени. Напомню, что время - одна из форм существования материи.
но закона, который бы описывал как этот самый процесс существует в этом самом времени, по тем или иным причинам, нам неизвестен. То есть, мы не можем написать какое-нибудь такое: X[t] = a + b*t + c*t^2 +...
Причины могут быть самые разные. Для примера возьмем рынок Forex. Так вот на нем даются изменения цен только в рабочие дни, то есть курс валют в выходные остается ненаблюдаемой величиной. (впрочем, есть некоторые форексманы, уверенные что в выходные валютный рынок не работает).
Зато у нас есть значения, которые процесс получает в определенные моменты времени. Что делать в этом случае? Выразить время через значения процесса... повторяться с линейной регрессией не буду... Замена переменной (в данном случае времени) - операция не приблизительная, а всегда точная! Слово "точная" нужно выделить маркером. Хотя, если тебя не устраивает, то ты волен использовать любые подходы.

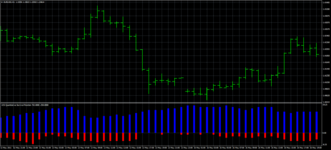
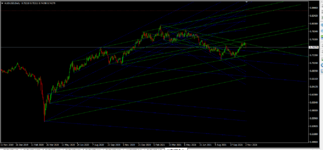
Ну, и маленько о веселом. Возьмем чего-нить хаотическое. Такое какое-нибудь

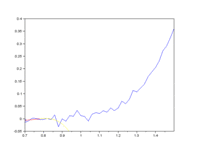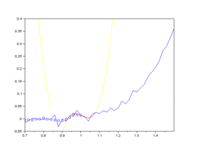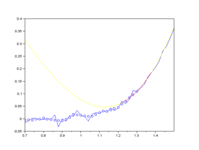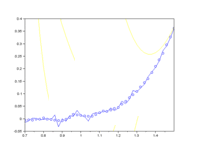
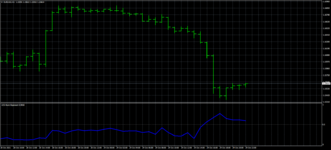
Можем ли мы это разобрать на части и хотя бы попытаться предсказать? Да как два байта отослать. Крайне простая операция - берем последовательные значения вот этого всего и переносим на двумерный график следующим образом. Пусть процесс описывается значениями p[0]...p[n]. Тогда точки будем делать так: 1-ая точка - x=p[0], y=p[1], вторая точка - x=p[1], y=p[2] и т.д. В результате, получаем такую картинку

в полученных пимпоках угадывается парабола. что немудрено - было использовано логистическое отображение.

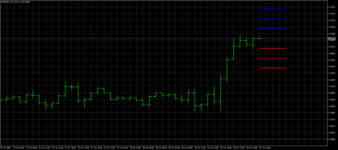
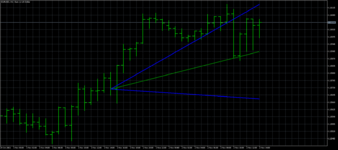
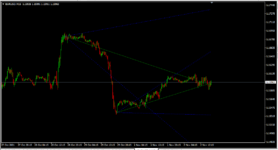
Ну, а теперь попробуем тот же фокус провернуть с ценами

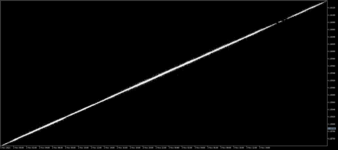
обратите внимание на толщину линий. Такая ситуация называется "жопой". Это такой научный термин, загуглите если чё. Это указывает на то, что характеристики описывающие движение цены "склонно к измене и к перемене, как ветер мая".

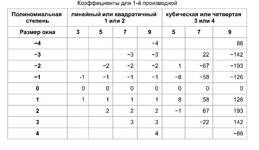
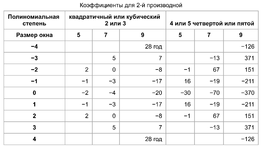
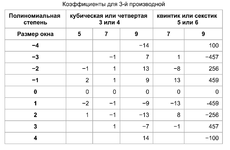
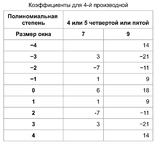
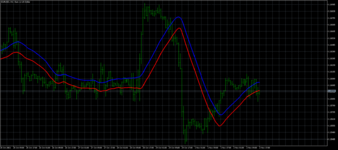
Ну, а закончим все это дело в позитивном ключе. Вот здесь скачиваем индикатор (вообще, умнейший человек такое придумал) https://forexsystemsru.com/threads/matematicheskie-osnovy-indikatorov.89867/post-1659662
и вставляем в него коэффициенты из нужного столбца

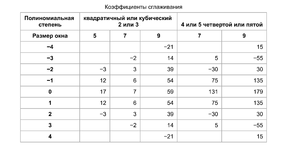
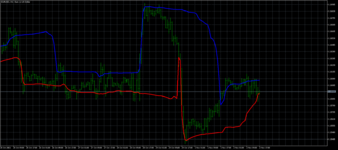
еще, можно взять индикаторы отсюда https://forexsystemsru.com/threads/matematicheskie-osnovy-indikatorov.89867/post-1679452 (тоже гениальнейший чел это придумал... увидите его - 10 баксов ему от меня передайте, да чё я жадничаю-то? - 20 баксов ему от меня дайте) вставляем в него разное

 

[panand]

Гляжу, кругом - благолепие и красота. Надоело, давайте сеять вокруг хаос и беспорядок. Раз есть гармоническое среднее, то должно быть и противогармоническое . И такое среднее есть и оно является частным случаем средних Лемера. Вот о них и будет данный индикатор.
Представьте, индикатор может работать и как обычное среднее, и как какой-то канальный... запросто. Что получится, зависит от параметра Exponent. 0 - смысла не имеет, 1 - обычная скользящая средняя, 2- контргармоничное среднее...
смотрим Exponent=2
Посмотреть вложение 453429
ну, в общем - чего-то сглаживающее Да и нормально. Но картина начинает меняться при повышении Exponent. Вообще, это среднее может служит детектором огибающей по точкам экстремумов. Вот тут Лемер просил кланяться и передавать привет строителям зигзагов. Представьте, какие у вас будут зигзаги, если сначала вы отфильтруете максимумы и минимумы с помощью этой средней.
Итак, Exponent = 1000
Посмотреть вложение 453431

привет Алекс!
не плохо бы линии отрисовать в реверс,будь синий или красный или оба,авось на пересечении их перст всевышнего укажет куда идти

 

[Bullra]

Ну, а теперь попробуем тот же фокус провернуть с ценами
Посмотреть вложение 453522
обратите внимание на толщину линий. Такая ситуация называется "жопой". Это такой научный термин, загуглите если чё. Это указывает на то, что характеристики описывающие движение цены "склонно к измене и к перемене, как ветер мая".

Да. Действительно похоже на жопу. Правда я сперва подумал, что это кто-то кокаиновую дорожку прочертил прямая баланса. Но раз жопа, так жопа. Пожалуй я ее даже сохраню и буду холодными зимними вечерами разглядывать под микроскопом.

 

[AlexeNP]

привет Алекс!
не плохо бы линии отрисовать в реверс,будь синий или красный или оба,авось на пересечении их перст всевышнего укажет куда идти

все реверсы были запрещены генеральным постановлением ООН на прошлой неделе... но можно так попробовать